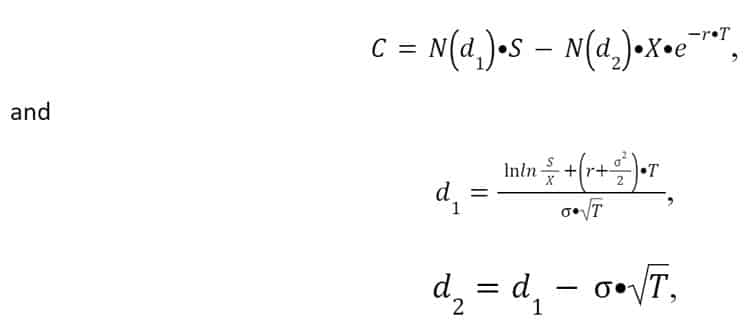Real options: evaluating investment projects in situations of uncertainty.

The method of evaluating alternative management options for complex projects, the implementation of which can compensate for a negative NPV.

Implementing complex technological projects is associated with high uncertainty and a significant risk of investment loss. And if the calculation of effectiveness shows a negative NPV, the obvious solution becomes a complete rejection of the proposed initiative. However, the discounted cash flow method is not the only, nor the most accurate, method of investment analysis for attractive, knowledge-intensive, and long-term projects.

In the standard analysis of the NPV method, two drawbacks can be identified:

1. The standard method does not take into account the influence of uncertainty on the analysis. There are two scenarios that allow for this: scenario analysis and sensitivity analysis. In scenario analysis, the investment project is evaluated under a small number of possible outcomes, while NPV analysis offers only one view of the future. Scenario analysis compares several alternative future scenarios. The approach to scenario analysis can also involve comparing different investment projects for their economic feasibility. The second scenario is sensitivity analysis. While scenario analysis examines only a few possible outcomes, this method analyzes the impact of uncertainty in input parameters on the analysis results. In scenario analysis, input values take only certain discrete values depending on the scenario, such as low and high market potential. In sensitivity analysis, these input data are complemented by the distribution of statistical uncertainty. This allows for systematically changing variables in the model to determine their impact on the final result.
2. The second drawback of the NPV method is its lack of flexibility. The project is considered as a “now or never” decision, without any opportunities for the decision-making company management to modify the project during its lifecycle. In a realistic business model, this condition is not met.

In our company, we use real options to solve such problems. It allows us to assess the potential economic efficiency of investment projects even under conditions of high uncertainty. Furthermore, real options help translate the intuitive assumptions of technical specialists about the benefits that a new project may bring in the future into the language of numbers.

Types of real options

The real options method is based on the assumption that any investment opportunity can be considered as a financial option: the company has the right, but not the obligation, to create or acquire assets within a certain period. Real options allow for changing and making optimal decisions in the future based on incoming information. The five most popular types of real options are:

1. Expansion option: Used when evaluating projects where investments can be made later upon the occurrence of favorable events. This type of option is analogous to a call option.
2. Contraction option: Provides the possibility of gradually reducing the business if a pessimistic scenario unfolds. It falls under the category of put options.
3. Abandonment option: Applied to analyze investment projects whose outcomes can be sold after a certain period following the initial investments. This option will be exercised when the current value of the assets falls below the liquidation value. It represents a put option.
4. Deferral option: In this case, investments can be deferred until additional information necessary for a more thoughtful decision is obtained. It belongs to the category of call options.
5. Compound options: These are combinations of different types of options that are executed in stages. The value of each subsequent option depends on the exercise of the previous ones.

The valuation algorithm.

Start the project efficiency analysis with the classical calculation of NPV. Then calculate the value of the real option. The total value of the project is the sum of NPV and the value of the option. Since real options are derivatives of financial options, the methods for valuing financial options have been adapted for evaluating real options.
There are at least three valuation methods:

1. the Black-Scholes formula,
2. the binomial method,
3. the Monte Carlo method.

The Black-Scholes formula is one of the most commonly used in the financial sector. It was originally developed to value European call options. The first fundamental assumption of the model is that the option can only be exercised at the end of the time period. To calculate the value of a put option using the Black-Scholes formula, the concept of put-call parity for European options is used. The sum of the value of the call option and the present value of its exercise price equals the sum of the value of the put option and the current value of the underlying asset.

The Black-Scholes formula for calculating the value of a call option is as follows:

N (d) – is the cumulative distribution function of the normal distribution;

S – is the price of the underlying asset (current value of cash flows from investments);

X – is the strike price (investment amount);

r – is the risk-free interest rate (in Western countries, it is typically government bonds, while in Russia, it is often the corporate deposit rate of Sberbank);

T – is the time to expiration (duration of the period during which a decision can be deferred or the time until the next decision point);

– is the volatility (the standard deviation of cash flows), representing the “variability of the asset price.” For real assets, the usual method of estimating this parameter is through the analysis of statistical data from past periods.

Upon closer examination of the two terms in the equation, two important components of the Black-Scholes model can be identified. The first term represents the expected benefit from immediate investment, while the second term reflects the value of the strike price payout at the expiration date, weighted by the probability of its execution. The formula also demonstrates the influence of time on the option’s value. Increasing T will lead to an increase in d1 and a decrease in d2, resulting in a higher option price.

To calculate the cost of a put option using the Black-Scholes formula, the concept of call-put parity for European options can be applied. This means that the sum of the call option’s cost and the present value (PV) of the strike price is equal to the sum of the put option’s cost and the current value of the underlying asset. The formula for calculation is presented below:

C + PV (X) = P + S,

С – cost of the call option;
Р – cost of the put option.

The parameter of the model that creates the most issues is project uncertainty (σ), expressed in percentages. In the case of financial assets, its magnitude is associated with the volatility of the underlying asset, such as stock prices or oil. Since these assets are traded in financial markets, their volatility can be easily calculated. However, in the case of real options, there is no existing market, and we cannot calculate volatility but can only estimate it expertly.

Another assumption of the Black-Scholes model is that the logarithm of NPV follows a Brownian motion. This assumption is reasonable for stocks but not for investment projects. Additionally, financial options are inherently independent of each other. The exercise of a put or call option does not influence the value of other options or the value of the underlying asset. However, real options typically interact with each other. For example, a company may have the option to expand its factory or sell it. If the second option is exercised, the parameter of scaling up loses its significance. The Monte Carlo method allows for more accurate forecasts, but it is a more complex calculation that not everyone can utilize.

Limitations of the method.

Method of real options is a valuable tool, but it has several limitations that need to be considered:

1. The higher the project uncertainty, the higher the option’s cost. Modern software allows assigning uncertainty to all input parameters, but it is important to focus on factors with the greatest expected impact, such as consumer response to a new product, technology lifespan, etc.
2. A real option typically reduces the risk of low payoffs but does not guarantee positive cash inflows. For example, in Monte Carlo analysis, thousands of potential future scenarios are calculated, and expert judgments are made based on the resulting probability distribution. However, if a project with an option for expansion turns out to be unprofitable, it will lead to the option having a zero value.
3. In real business, decision-making cannot be indefinitely postponed. Real options analysis always assigns great value to waiting. In a project where investment can be delayed, the option brings significant value. This effect is illustrated, for example, in the Black-Scholes formula. However, in practice, the threat of competitors entering the market pushes decision-makers to act as quickly as possible. In real conditions, the value of waiting diminishes rapidly because the advantage usually goes to those who take the first step.

Written by Anna Bolotova.

Have you read?
The highest-paid tech CEOs in the United States.
Highest-Paid Biopharmaceutical CEOs in the United States.
Executive Pay: Top 8 Highest-Paid Hotel CEOs.
Openly LGBTQ CEOs at the helm of major global companies.
Top countries that admire their CEOs and other C-suite leadership teams the most.
Top Women CEOs of America’s largest public companies (2023 List).
Ready to join the CEOWORLD magazine Executive Council– Find out if you are eligible to apply.

This report/news/ranking/statistics has been prepared only for general guidance on matters of interest and does not constitute professional advice. You should not act upon the information contained in this publication without obtaining specific professional advice. No representation or warranty (express or implied) is given as to the accuracy or completeness of the information contained in this publication, and, to the extent permitted by law, CEOWORLD magazine does not accept or assume any liability, responsibility or duty of care for any consequences of you or anyone else acting, or refraining to act, in reliance on the information contained in this publication or for any decision based on it.

Email Address*

Name