Proper Money Calculus

In (business) economics one often has to deal with amounts of money at different points in time. One cannot say much about main economical issues without proper money calculus.

Using PPR (Period Percentage Rate, any period, any rate) i.e. Discrete Compound Interest to rank investments is often deceptive. Financial tools like Microsoft Excel using PPR are dangerous. At many schools and universities worldwide, the teaching of financial calculus can, and should be improved. The mean of amounts of money at different dates or whatever “calculation”, which does not do justice to the ‘present value’ of money, is artificial. Balance sheets stating long term liabilities at face value are fiscally and otherwise acknowledged as ‘de jure’, but ‘de facto’ economically speaking, those balance sheets are beyond reality.

Re ‘Accounting Real Interest‘ and to learn it from the beginning, see Chapter 2 in ISBN 9781086355635 available at Amazon.

Here the content of the book is given:

Interest rates are either continuous or discrete. Continuous rates together with continuous interest formulas or discrete rates with discrete formulas. It does not matter (‘au fond’) which one you choose. From a calculation in the discrete way can be switched over to calculating continuously and vice versa without any change in outcomes as long as one calculates exactly. The (correct) calculation itself creates no difference at all. You only cannot mix both. Continuous rates do not fit into discrete formulas nor do discrete rates fit into continuous formulas. Often for instance by Microsoft Excel one makes a mess by mixing these up. Re free downloadable ‘Microsoft Excel, Financial Functions, Matter in Dispute‘.

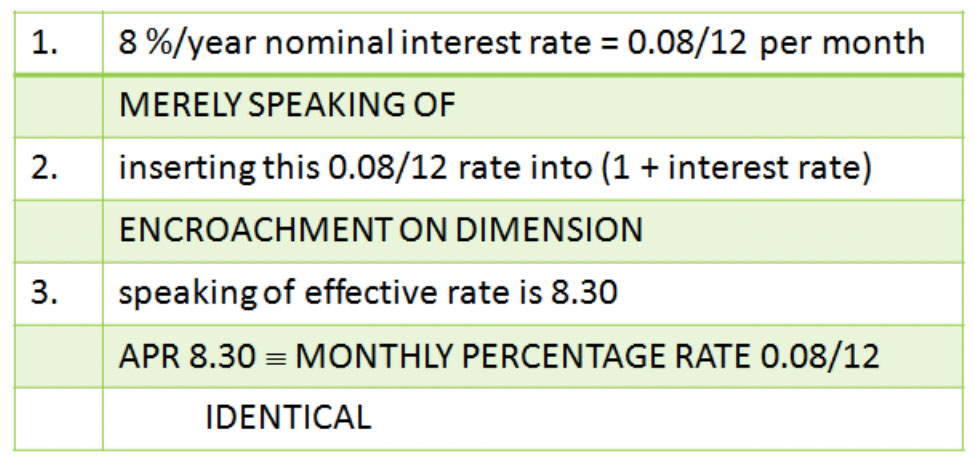
An interest formula with (1 + interest rate) for instance function PV in Microsoft Excel means that the ‘interest rate’ cannot have a dimension.

Excel states 0.08/12 = 0.00666666… and gives the answer 59,777.15 to the PV of monthly payment 500, during 20 years, whereas annual rate is 8 %. Via (1.00666666…)^12 = 1.08299950… the used MPR (Monthly Percentage Rate) can be transformed into the equal APR (Annual Percentage Rate) 8.299950… %; to two decimal places 8.30 %.

Whereas Excel states 0.08/12 = 0.00666666… this rate must be the continuous i

→    B at 0 = 59,658.4570…

Microsoft Excel starts with 8 %/year and ends up with B at 0 = 59,777.15

That does not make sense. Either you start with 8 %/year but then you get B at 0 = 59,658.46 or starting with 0.08/12 monthly discrete interest rate the answer is B at 0 = 59,777.15 but in this case the corresponding annual discrete interest rate is 8.30 %. Not 0.08 but 0.083. Just a number, no more, no less.

If indeed 8 % annual discrete interest rate then the corresponding monthly discrete interest rate is 0.6434… % → B at 0 = 61,038.87

These are not just slight differences. The differences are significant. The so-called effective interest rate in Microsoft Excel is NOT the effective rate! A discrete rate, any discrete rate can never be effective. The word ‘effective’ means real, true, truly, i.e. there can be only one effective rate. According to the opinion of some scientists annual rates can be or even must be named ‘effective’. Why ‘one year’? There is no science in it. An amount of money is growing as time goes by. A growing process all of the time. Never a dull moment. It does not grow faster in some periods and slower at other moments. It grows steadily, well described by the e-power. There are many more growth processes described by the e-power. The process of capital growth is just one of the applications using the formula FV at t = PV at 0  · e^i.t and this i (only this i) is the effective rate. Not my definition, not a definition by mankind, but the one and only truth. Proven, see mathematics and observations of growth processes in practice. Science is trying to find such regularities. Usually there is little science in definitions.

By making calculations with the e-power, the most precise answers on all money calculus can easily be found in the least necessary steps. Every step in calculations is dangerous because at each step accuracy may be lost. Moreover, i is a fraction, so i = 12 %/year = 1 %/month. Discrete interest rates are not fractions and that is where all the misery starts. Economists are mostly not accustomed to take into account dimensions. What Microsoft Excel (and other financial tools as well) is calculating: ([1] + [1/TIME]) is not allowable.

In the US it is common practice  to speak of an 8 % nominal rate when the so-called effective rate (APR) is 8.30. The US Congress attempted to remedy the situation with the passage of ‘Truth-in-Lending’ in 1967. There are detailed regulations (‘Regulation Z’) that explicitly set forth the formulas to be used and what items are to be considered in calculating interest. In general, results are stated as an APR (Annual Percentage Rate).

Microsoft claims: The problem is not Excel; XL is applying the correct formulas. The problem is that many of the people using XL and other financial tools are not aware of the distinctions between “effective” and “nominal” interest.

Summons: Lay i down asap in constitutions all over the world to make it crystal clear to everybody for ever. To make calculations short and easy. To minimize costs. To improve capital budgeting decisions.

Meanwhile Microsoft Excel is in a tight situation between what is proven science on the one hand and on the other ‘Regulation Z’.

Microsoft Excel is NOT applying the correct formulas and is NOT aware of the distinctions between “effective” and “nominal” interest, broadcasting:

If APR 8.30 is called ‘effective’ then the same qualification applies to the rate on the right of this equation and to innumerable other rates. Hence APR 8.30 cannot be the effective rate.

Watch out, be careful, when undertaking financial calculations.

Commentary by Jan Jacobs. Here’s what you’ve missed?
World’s Best Destinations For Business Travelers.
World’s Most Stressed-Out Cities For Employees.
The World’s Best Luxury Superyacht Charters And Builders.
Luxury Superyacht charter in Greece and the Greek Islands.
Crewed MegaYacht charter in Greece and the Greek Islands.